Cómo calcular el ángulo teta en trigonometría

Guardar

triangle image by Zbigniew Nowak from Fotolia.com

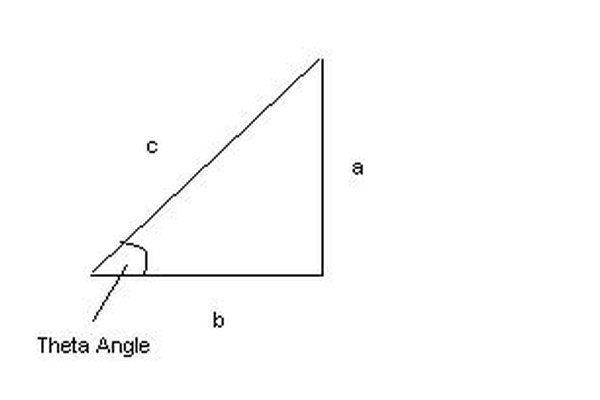
La trigonometría es el estudio matemático de los triángulos. En trigonometría, la medida del ángulo desconocido en el triángulo se llama triángulo teta. La medida del ángulo teta se puede determinar utilizando identidades trigonométricas.

Identifica el ángulo teta, el ángulo desconocido del triángulo.

Identifica los lados "a", "b" y "c" del triángulo. El lado "a" es el lado opuesto del ángulo teta. El lado "b" es el lado adyacente al ángulo teta. El lado "c" es la hipotenusa, o el lado más largo del triángulo.

Selecciona una identidad trigonométrica para calcular el ángulo teta, dependiendo de las longitudes de los lados conocidos. Las identidades trigonométricas son las siguientes: 1. Sen (q) = a/c 2. cos (teta) = b/c 3. tg (teta) = a/b

Conecta las longitudes de los lados de la identidad trigonométrica seleccionada para determinar su relación. Por ejemplo, si el lado a = 6 y el lado c = 10, entonces sen (teta) = 6/10 o 0,6.

Usando una calculadora científica o gráfica, utiliza la relación de la identidad para determinar la medida del ángulo teta. En la calculadora, selecciona sin ^ -1, cos ^ -1, o tan ^ -1, dependiendo de la identidad trigonométrica utilizada, luego, escribe la relación del paso 4. La respuesta a esta función es la medida del ángulo teta. Por ejemplo, si sen (teta) = 0,6, entonces sen ^ -1 (0,6) = 36,9, y el ángulo teta medirá 36,9 grados.