Cómo hacer una espiral a partir del Teorema de Pitágoras

Una de las virtudes de la geometría, desde la perspectiva de un maestro, es que es altamente visual. Por ejemplo, puedes tomar el Teorema de Pitágoras -un bloque fundamental de la geometría- y aplicarlo para construir una espiral similar a la de un caracol con un número de propiedades interesantes. A veces llamada espiral de raíz cuadrada o espiral de Teodoro, esta invención engañosamente sencilla demuestra las relaciones matemáticas de una forma bastante llamativa.

Un repaso rápido al Teorema

El Teorema de Pitágoras establece que en un triángulo de ángulo recto, el cuadrado de la hipotenusa es igual al cuadrado de los otros dos lados. Expresado matemáticamente, esto significa que A² + B² = C². Siempre y cuando conozcas los valores de cualquiera de los dos lados de un triángulo recto, puedes usar este cálculo para llegar al valor del tercer lado. La unidad de medida que escojas puede ser cualquiera desde pulgadas hasta millas, ya que la relación sigue siendo la misma. Es importante recordarlo ya que no necesariamente tendrás que trabajar con una medida física siempre. Puedes definir una línea de cualquier longitud como "1" para propósitos de cálculo y luego expresar cualquier otra línea mediante su relación con la medida escogida. Así es como la espiral funciona.

Iniciando la espiral

Para construir la espiral, haz un triángulo rectángulo con lados A y B de igual longitud, los cuales se convierten en el valor "1". Ahora, haz otro triángulo rectángulo usando el lado C de tu primer triángulo (la hipotenusa) como el lado A de tu nuevo triángulo. Mantén el lado B de la misma longitud que tu valor escogido de 1. Repite el mismo proceso de nuevo, usando la hipotenusa del segundo triángulo como el primer lado del nuevo triángulo. Toma 16 triángulos para regresar al inicio donde la espiral debería comenzar a sobreponerse sobre tu punto inicial, el cual es el punto donde el antiguo matemático Teodoro se detuvo.

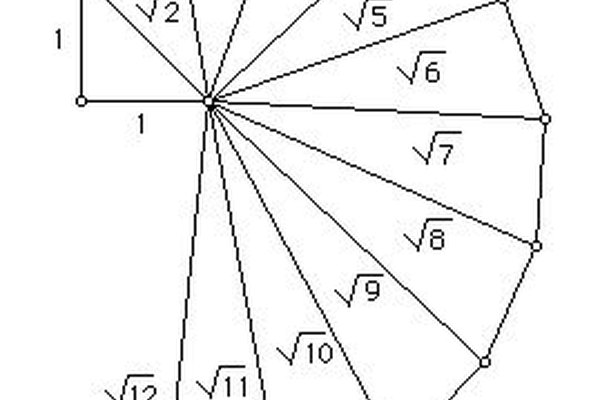
La espiral de raíz cuadrada

El Teorema de Pitágoras nos dice que la hipotenusa del primer triángulo debe ser la raíz cuadrada de 2, porque cada lado tiene un valor de 1 y el cuadrado de 1 sigue siendo 1. De esta forma, cada lado tiene un área de 1 al cuadrado, y cuando estos se suman, el resultado es 2 al cuadrado. Lo que hace a la espiral interesante es que la hipotenusa del siguiente triángulo es la raíz cuadrada de 3, y la siguiente después es la raíz cuadrada de 4, y así sucesivamente. Esto es el por qué es conocido como la espiral de raíz cuadrada, en vez de la espiral Pitagórica o la espiral de Teodoro. En la práctica, si estás planeando crear una espiral al dibujar en papel o cortando triángulos de papel y colocándolos en un cartón, puedes hacer el cálculo de antemano para saber cuán grande puede ser tu valor de 1 para que la espiral se ajuste a la página. Tu línea más larga será la raíz cuadrada de 17, para cualquier valor de 1 que escojas. Puedes trabajar al revés, desde el tamaño de tu página, para encontrar un valor adecuado de 1.

La espiral como una herramienta de enseñanza

La espiral tiene un número de usos en el salón de clases o en tutorías, dependiendo de la edad de los estudiantes y su familiaridad con los fundamentos de la geometría. Si sólo estás introduciendo los conceptos básicos, crear la espiral es un útil tutorial del teorema de Pitágoras. Por ejemplo, podrías hacer que hagan los cálculos basados en valores de 1 y luego usar una regla del mundo real en centímetros o pulgadas. El parecido de la espiral con un caparazón de un caracol brinda la oportunidad de analizar las relaciones matemáticas que aparecen en el mundo natural y, para los niños más pequeños, se presta a coloridos esquemas decorativos. Para estudiantes avanzados, la espiral demuestra el número de relaciones intrigantes a medida que continúa dando vueltas.

Este artículo fue realizado con la ayuda de sciencing.com