Cómo calcular la catenaria

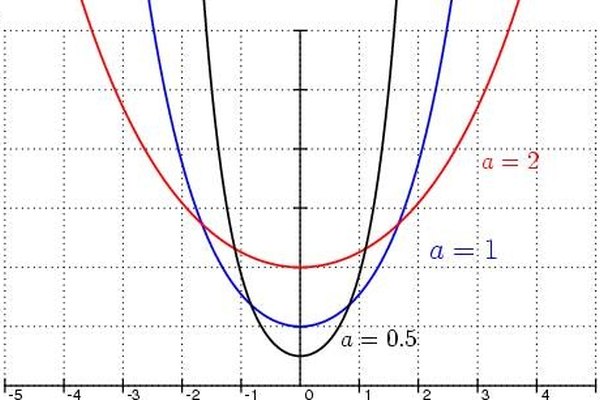
Una catenaria es la forma que adopta un cable cuando está apoyado en sus extremos y solamente actúa por su propio peso. Se utiliza mucho en construcción, especialmente para la suspensión de puentes, y una catenaria invertida ha sido utilizada desde la antigüedad para construir arcos. La curva de la catenaria es la función del coseno hiperbólico que tiene una forma similar a una U de la parábola. La forma específica de una catenaria podría estar determinada por su factor de escala.

Calcula la función catenaria estándar y = a cosh(x/a) donde "y" es la coordenada cartesiana "y", "x" es la coordenada cartesiana "x", "cosh" es la función del coseno hiperbólico y "a" es el factor de escala.

Observa el efecto del factor de escala en la forma catenaria. Este factor podría estar pensado como el cociente entre la tensión horizontal en el cable y su peso por unidad de longitud. Por lo tanto, un factor de escala bajo podría tener como resultado una curva más profunda.

Calcula la función catenaria con una ecuación alterna. La ecuación y = a cosh(x/a) puede mostrarse como equivalente matemáticamente a y = a/2 (e^(x/a) + e^(-x/a)), donde "e" es la base del logaritmo natural y su valor es aproximadamente de 2,71828.

Calcula la función para una catenaria elástica como y = yo/(1 + et), donde "yo" es la masa inicial por unidad de longitud, "e" es la constante de elasticidad y "t" es el tiempo. Esta ecuación describe una elasticidad rebotante en lugar de un cable colgante.

Calcula un ejemplo del mundo real de una catenaria. La función y = -127,7 cosh(x/127,7) + 757,7 describe el Arco de San Luis donde las medidas están expresadas en pies.