Cómo saber si existen límites en el gráfico de una función

El límite de una función real estudia el comportamiento que tienen las imágenes de la función f(x) cuando la variable de “x” se acerca a un valor “c”, es decir, a medida que “x” se aproxima a “c” las imágenes de f(x) se acercan a “L”, donde “L” es el límite.

Ekuatio.com define al límite matemático de una forma simple cuando nos argumenta que el límite es determinar un valor al que se aproxima una función cuando “x” tiende a un punto “c” pero sin llegar a (tocar) ese punto.

Simbólicamente el límite en matemáticas se escribe fx=L .

La expresión fx=L se lee de la siguiente forma:

El límite de la función f cuando “x” tiende a “c” es igual a L. Cuando decimos que “x” tiende a “c” intrínsecamente se estudian los límites laterales (por la derecha o por la izquierda).

De esta manera el límite por la derecha se escribe simbólicamente así: fx y estudia el comportamiento de las imágenes de la función f(x) para los valores de “x” cercanos a “c” por la derecha.

Mientras que el límite por la izquierda se escribe simbólicamente así fx y estudia el comportamiento de las imágenes f(x) para los valores de “x” cercanos a “c” por la izquierda.

Al estudiar los límites de una función en sus laterales se determina que el límite exista y sea único.

Ahondemos en la definición del límite en el gráfico de una función y otros conceptos matemáticos afines.

No dejes de leer: ¿De qué forma la matemática está involucrada en el diseño de videojuegos?

Definición del límite en términos épsilon- delta (ɛ-δ)

El matemático alemán Karl Weierstrass (1815-1897), propuso la definición de límite matemático en términos de ɛ-δ, así:

“si es posible determinar una cota δ tal que para todo valor h, más pequeño en valor absoluto que δ, f(x +h)- f(x) sea más pequeña que una cantidad tan pequeña ɛ como se quiera, entonces se dirá que se ha hecho corresponder a una variación infinitamente pequeña de la variable una variación infinitamente pequeña de la función”.

Tanto Augustin Cauchy como Weierstrass dedicaron una gran parte de sus meditaciones a colocar esa noción sobre una base lógicamente sólida y así darle cierta “exactitud lógica”, independiente de toda intuición geométrica.

Esta definición rigurosa del límite es la siguiente: Sea f una función definida en un intervalo abierto que contiene a “c” (salvo posiblemente en c) y L un número real. La afirmación:

fx=L

Significa: par todo ɛ>0, existe un δ>0 tal que, si 0<|x-c|< δ entonces |f(x)-L|< ɛ. Gráficamente la definición de límite en términos de épsilon-delta se visualiza de la siguiente manera:

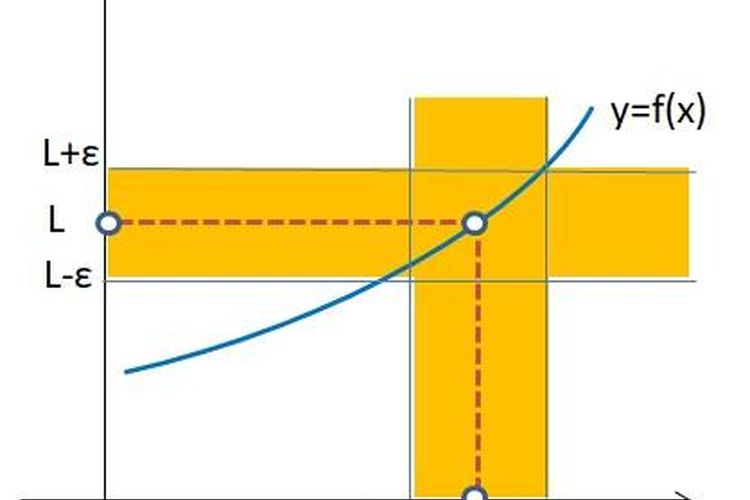
La definición de límite en términos épsilon-delta (ɛ-δ) es utilizada para las demostraciones en las asignaturas del cálculo (infinitesimal) y el análisis matemático.

Hoy día es llamada definición formal del límite, base primordial para el concepto de continuidad, derivadas e integrales de funciones reales.

Te puede interesar: Definición de funciones matemáticas para Excel

Procedimientos para hallar el valor de un límite

A continuación, explicaremos los tres procedimientos básicos para hallar el valor de un límite.

Valor de un límite en matemáticas (por procedimiento numérico)

La noción numérica sobre el límite en matemáticas se debe al matemático francés Augustin Louis Cauchy (1789-1857), definida así:

“Cuando los valores sucesivamente atribuidos a una misma variable se aproximan indefinidamente a un valor fijo, de manera que llegan a diferir tan poco como se quiera de él, este último se llama el límite de todos los demás”.

Para una mayor comprensión estimaremos por medio de un ejercicio en particular el valor del límite 3x+5 haciendo uso del procedimiento numérico.

Valor del límite procedimiento numérico ejemplo:

Por la vía numérica, hallaremos el límite de f(x) = 3x+5 cuando “x” tiende a 1.

Para ello, se elabora una tabla tomando tres valores próximos a la izquierda de x=1 (0,9; 0,99 y 0,999).

Luego se hallan las imágenes de “f(x)” en cada uno de los puntos (f(0,9); f(0,99); f(0,999)) y se observa que los valores de las imágenes se acercan a 8.

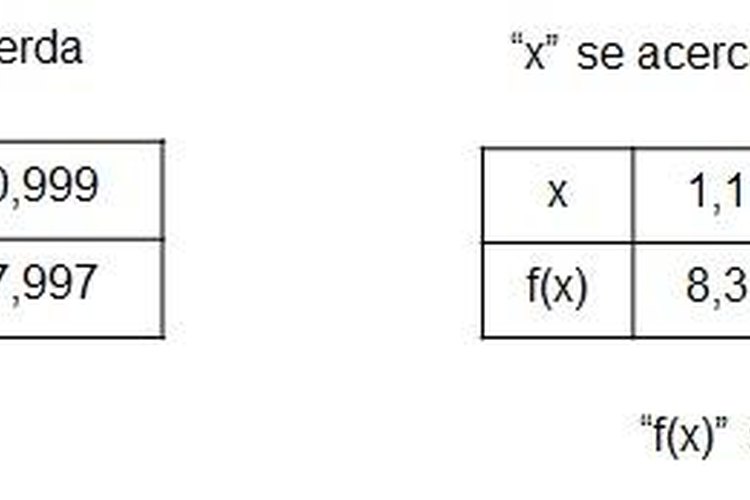
Del mismo modo se procede a elaborar una tabla tomando tres valores próximos a la derecha de x=1 (1,001; 1,01; 1,1).

Posteriormente se hallan las imágenes “f(x)” en cada uno de los puntos (f(1,001); f(1,01); f(1,1)) y se observa que los valores de las imágenes se acercan también a 8.

Con este proceso se estudia el comportamiento numérico del límite y se concluye que a medida que “x” se acerca a 1 por la izquierda o por la derecha, las imágenes de f(x) se acercan arbitrariamente a 8. Por lo tanto el 3x+5 existe y su valor es 8.

La tabla obtenida es la siguiente:

Hallar el valor de un límite por la gráfica

Hablar del concepto de límites en matemáticas en su noción intuitiva geométrica (vía gráfica) se remonta a los aportes de Newton y Leibniz en el siglo XVII y XVIII sobre los métodos del cociente diferencial y de las fluxiones.

Aunque esta noción no era muy precisa para aquellos tiempos es la que hoy día se maneja al estudiar el límite de una función f(x) alrededor de un punto “c”, es decir, fx=L . Gráficamente la podemos se visualiza así:

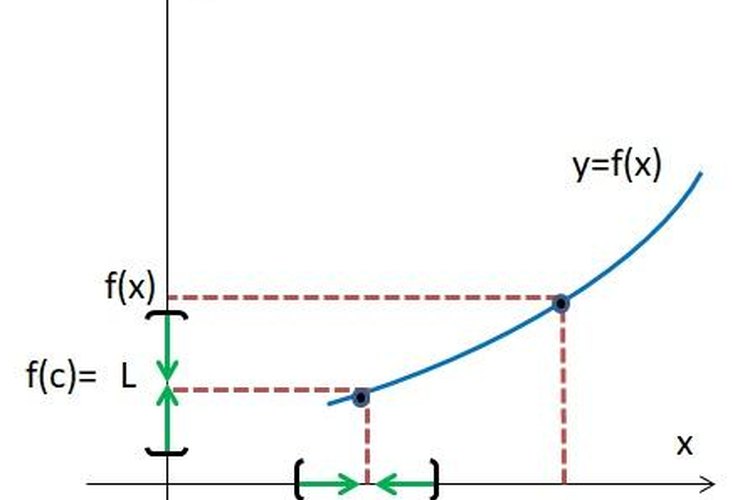
Es importante aclarar que f(c) estudia el comportamiento de la función f en el valor de “c”, mientras que fx estudia el comportamiento de la función alrededor del valor “c”. De esta manera el límite se estudia alrededor de un punto no en el punto.

Para una mayor comprensión estimaremos por medio del siguiente ejercicio el valor del límite 3x+5 utilizando el procedimiento gráfico.

Te puede interesar: ¿Cómo calcular raíces con MATLAB?

Límite en el gráfico de una función

El objetivo clave en primer lugar es graficar la función f(x)=3x+5. Como se trata de una función lineal o un polinomio de primer grado, basta con hallar dos puntos y graficar la recta.

Para ello, tomaremos los puntos de intersección (x=0, y=0) obteniendo (0, f(0)=5) y (x=-5/3, 0).

La gráfica de f(x) asociada es la siguiente:

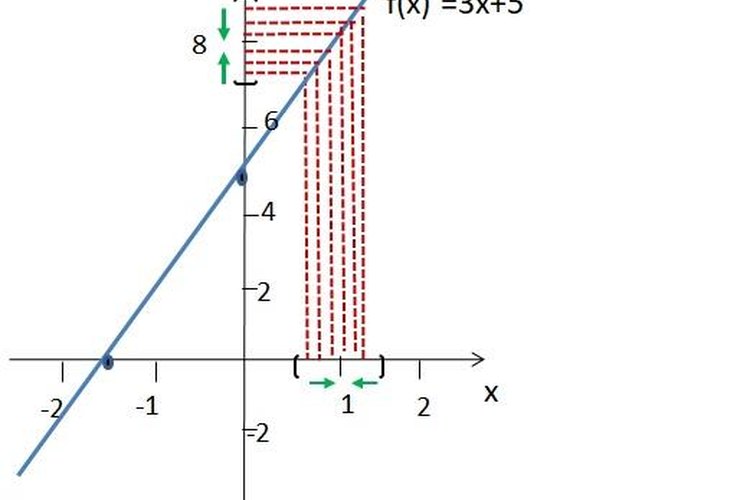
Luego, obtenida la gráfica de la función f(x)=3x+5 nos abocamos a estudiar el comportamiento de las imágenes de “f(x)” alrededor de x=1, es decir, 3x+5 .

Podemos observar como las imágenes de “f(x)” alrededor de x=1 se aproximan a 8, no presentando saltos o crecimientos o decrecimientos hacia el infinito o menos infinito.

Por lo tanto, decimos que el límite lateral por la derecha, como por la izquierda, se aproximan a 8 y se determina que el límite existe y es único.

Te puede interesar: ¿Cómo calcular el valor de la pendiente de la regresión de cuadrados mínimos en Excel?

Límite de una función por procedimiento analítico

Para abordar este tipo de procedimiento y estimar el valor de un límite, primero se deben manejar las siguientes propiedades básicas de los límites:

Sean b,c números reales, n un número entero positivo, f y g funciones.

1. Múltiplo escalar, b=b , el límite de una constante es una constante.
2. Constante por función, bf(x)=bf(x)  , el límite de una constante o número real por una función es igual a multiplicar la constante por el límite de la función.   
3.  Suma o diferencia, fx±gx=fx± gx ,  el límite de la suma o diferencia de dos funciones es igual a la suma o diferencia de los límites de cada función.
4. Producto, fxgx=fx gx ,   el límite del producto de dos funciones es igual al producto de los límites de cada función.
5.  Cociente, f(x)gx = f(x) g(x) , siempre y cuando g(x) ≠0, el límite del cociente de dos funciones es igual al cociente de los límites de cada función.
6. Potencia, f(x)g(x)=[limx→cfx]x→c g(x)  , el límite de una potencia es igual al límite de la base elevado al límite del exponente.

Con el uso de estas propiedades y las operaciones algebraicas se puede calcular el valor numérico exacto del límite de una función alrededor de un punto, prescindiendo del gráfico o de aproximaciones.

Hallar el límite de una función por procedimiento analítico

Abordaremos el siguiente ejemplo para hallar el límite, calcule 2x+3 .

Comenzaremos aplicando la propiedad número tres, que trata de suma o diferencia de límites.

Aplicando la propiedad que se tiene que 2x+3 = 2x+ 3 , luego se aplica la propiedad número dos (constante por una función) y así 2x+ 3 = x+ 3 .

Por último haciendo uso de la propiedad número uno (Múltiplo escalar) y evaluando x=1 en donde están las “x” se tiene 2x+3 =2*1+3=5.

De esta manera, se obtiene el valor numérico exacto del límite de f(x)=2x+3, cuando “x” tiende a 1, cuyo valor es 5.

Tal vez te interese: ¿Cómo añadir una leyenda a un gráfico de Excel?

¿Cuándo un límite no existe?

Sabemos que un límite no existe cuando las imágenes de f(x) en los valores cercanos a “x=c” por la derecha y por la izquierda no se aproximan a un mismo valor.

Así las imágenes f(x) presentan saltos o crecimientos o decrecimientos abruptos hacia el infinito o menos infinito.

Hay tres tipos distintos de formas de saber si un límite existe mirando el gráfico de una función.

Saber si el límite no existe, método 1

La primera, f(x) crece o decrece sin cota cuando “x” tiende a “c”, es decir, que las imágenes de “f” se hacen cada vez más grandes, o más pequeñas, cuando “x” asume valores cercanos a “c”.

Veámoslo gráficamente:

En este caso en particular, a medida que “x” se acerca a 1 por la izquierda, las imágenes f(x) decrecen sin cota, por lo tanto fx no existe. Luego, a medida que “x” se acerca a 1 por la derecha, las imágenes f(x) crecen sin cota, por lo tanto fx no existe el límite.

En conclusión, fx no existe.

No dejes de leer: Tutorial sobre funciones matemáticas en Visual Basic

¿Cuándo un límite no existe? Método 2

El segundo caso, f(x) oscila entre dos valores fijos cuando “x” tiende a “c”.

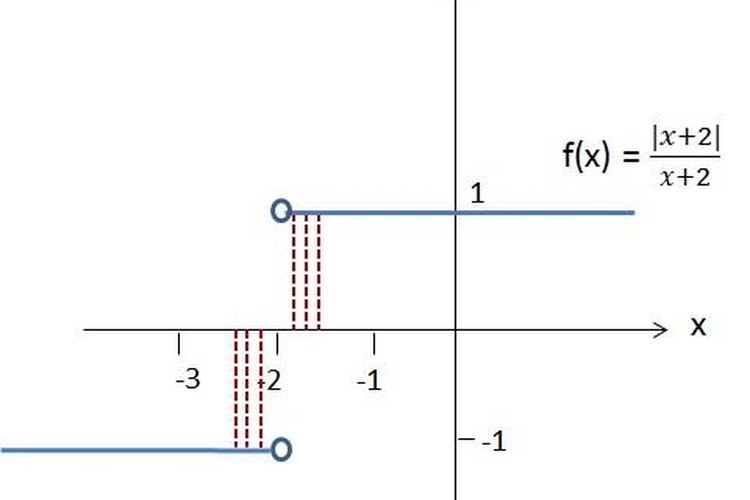
Podemos observar que a medida que “x” se acerca a -2 por la derecha, las imágenes f(x) son 1, por lo tanto fx=(1)=1 .

Luego, a medida que “x” se acerca a -2 por la izquierda, las imágenes f(x) son -1, por lo tanto, fx=(-1)= -1 .

En conclusión, fx no existe el límite.

No existencia del límite matemático. Método 3

Ahora en cuanto al tercer tipo cuando f(x) tiende a números diferentes según “x” tiende a “c” por la derecha o por la izquierda.

Veamos el siguiente gráfico:

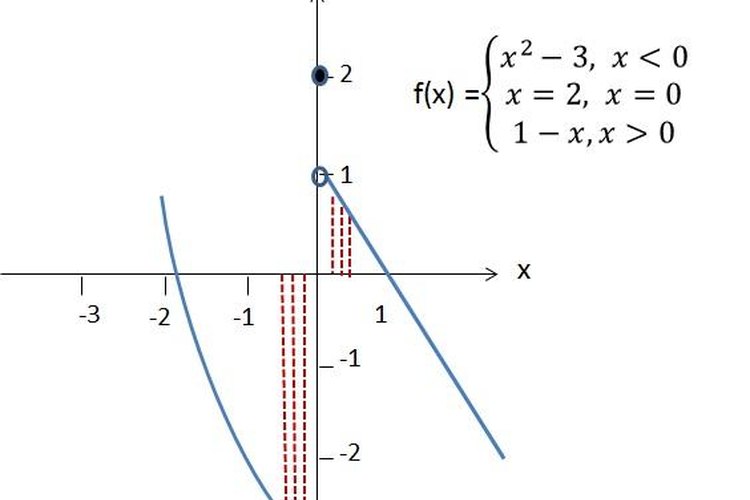
Se observa que a medida que “x” se acerca a 0 por la izquierda, las imágenes f(x) se acercan a -3, por lo tanto, fx=(x2-3)=-3 .

Por otro lado, a medida que “x” se acerca a 0 por la derecha, las imágenes f(x) se acercan a 1, por lo tanto fx=(1-x)= 1 .

De tal manera, que el límite de la función f(x) cuando “x” tiende a 0 no existe, así fx no existe.

Te puede interesar: Definición de funciones matemáticas para Excel

¿Qué es un límite en el infinito?

Hablar de límite en el infinito implica estudiar el límite de una función cuando “x” tiende a valores muy grandes o muy pequeños mientras las imágenes se encuentran más próximas al valor del límite.

Simbólicamente fx=L significa que para cada épsilon > 0 existe M > 0 tal que |f(x)−L| < ε siempre que x > M.

De tal manera, que a medida que “x” asume valores más grandes las imágenes f(x) se encuentran más próximas al valor de L.

Ahora si estudiamos fx=L significa que para cada épsilon > 0 existe N < 0 tal que |f(x)−L| < ε siempre que x < N.

De tal manera, que a medida que “x” asume valores más pequeños las imágenes f(x) se encuentran más próximas al valor de L.

Analicemos el siguiente ejemplo para calcular y observar con detalle la diferencia de estudiar un límite de una función cuando “x” tiende a un punto fijo a cuando “x” tiende a valores muy grandes o muy pequeños, es decir, no a un valor fijo.

Límite al infinito, ejemplo:

Sea f(x)=1/x +1, estudiaremos el comportamiento de la función para valores de “x” muy grandes y muy pequeños, es decir, hallaremos fx y fx .

Primero por medio del procedimiento numérico tenemos:

Se observa que a medida que “x” toma valores muy grandes, las imágenes f(x) se acercan arbitrariamente a 1.

Por lo tanto, 1x+1)=1 .

Del mismo modo, a medida que “x” toma valores muy pequeños, las imágenes f(x) se acercan arbitrariamente a 1, por lo tanto, 1x+1)=1 .

Así, el 1x+1)=1.

Ahora estudiando el límite en el infinito para este ejemplo en particular por procedimiento gráfico, se visualiza la existencia del límite de la función para valores de “x” muy grandes y muy pequeños, el cual se acerca a f(x)=1 pero de forma asintótica.

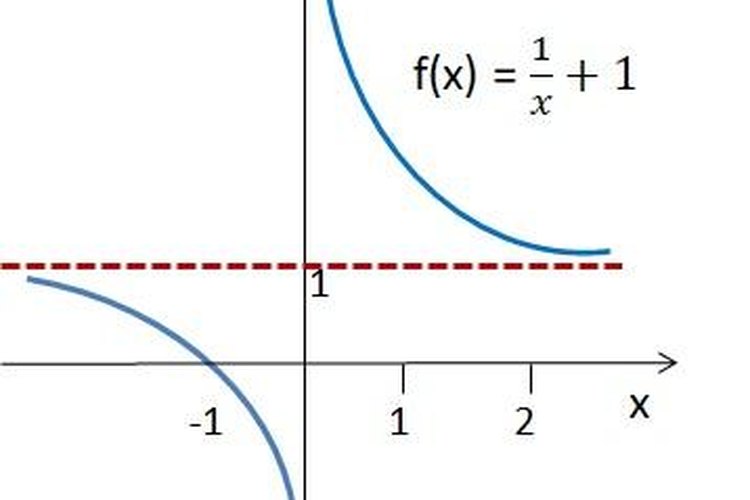
Esperemos que estas definiciones de límite y ejemplos gráficos te permitan abordar con mayor propiedad el tema.

Practica la existencia del límite en el gráfico de una función aprendiendo a graficar funciones en Microsoft Excel.